2015人教版初中物理专题练习108752
初中
整体难度：偏难
2015-04-08
题号
一
二
三
四
五
评分
一、计算题 (共7题)
添加该题型下试题
1.
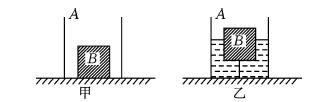
如图甲所示，水平旋转的平底柱形容器A的底面积为200 cm2，不吸水的正方体木块B重
为5 N，边长为10 cm，静止在容器底部，质量体积忽略的细线一端固定在容器底部，另一端固定在木块底面中央，且细线的长度为L＝5 
cm，已知水的密度为1.0×103 kg/m3.求：
（1）甲图中，木块对容器底部的压强多大？
（2）问容器A中缓慢加水，当细线受到拉力为1 N时，停止加水，如图乙所示，此时木块B受到的浮力是多大？
（3）将图乙中与B相连的细线剪断，当木块静止时，容器底部受到水的压强是多大？
难度：
知识点：压强和浮力单元测试
使用次数：326
【答案】
（1）F=G=5 N，
S=0.1 m×0.1 m=0.01 m2
＝
=500 Pa；
（2）木块B现在在水中受到竖直向上的浮力和竖直向下的重力、拉力，在这三个力的作用下处于静止状态，故F浮=G+F拉=5 N+1 N=6 N；
（3）据（2）可知F浮=6 N；故此时木块浸入水中的体积是：
F浮=ρgV排，V排=F浮/（ρg） =6 N/(1 000 kg/m3×10 N/kg)=0.000 6 m3；
故此时木块浸入水中的深度是：
h=V/S=0.000 6 m3/0.01 m2 =0.06 m=6 cm；
故此时液面的总高度是：h=6 cm+5 cm=11 cm；
故此时杯中水的体积是：
V=0.02 m2×0.11 m-0.000 6 m3=0.001 6 m3
将图乙中与B相连的细线剪断，当木块静止时，木块恰好处于漂浮状态，即此时F浮=G物=5 N；
V排=F浮/（ρg） =5 N/(1 000 kg/m3×10 N/kg)=0.000 5 m3；
故此时水和木块浸入水中的总体积是：
V=0.001 6 m3+0.000 5 m3=0.002 1 m3；
所以此时的液体的深度是：
h=0.002 1 m3/0.02 m2 =0.105 m；
故此时容器底部所受的压强是：
p=ρgh=1 000 kg/m3×10 N/kg×0.105 m=1 050 Pa.
2.
1.如图甲所示，弹簧测力计下面挂一实心圆柱体，将圆柱体从盛有水的容 器上方离水面某一高度处缓缓下降（其底面始终与水面平行），使其逐渐浸没入水中某一 深度处.如图乙是整个过程中弹簧测力计的示数F与圆柱体下降高度h变化关系的数据图像.已知ρ水=1.
0×103 kg/m3，g取10 N/kg.求：
（1）圆柱体的重力.
（2）圆柱体浸没时受到的浮力.
（3）圆柱体的密度.
（4）圆柱体在刚浸没时下表面受到的水的压强.
难度：
知识点：压强和浮力单元测试
使用次数：575
【答案】
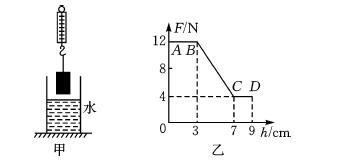
（1）由图像可知，当h=0时，弹簧测力计示数为12 N，此时圆柱体处于空气中，根据二力平衡条件可知，G=F拉=12 N；
（2）图像中CD段是圆柱体完全浸入水中的情况，此时圆柱体受到的拉力F=4 N，
则圆柱体受到的浮力F浮=G-F=12 N-4 N=8 N.
（3）圆柱体完全浸入水中时根据F浮=ρ水gV排得：
V物=V排=
=
=8×10-4 m3，
由公式G=mg可求出物体的质量
m=
=
=1.2 kg，新$课$标$第$一$网
则圆柱体密度
ρ物=
=
=1.5×103 kg/m3.
（4）由图像可知，不考虑水面上升，圆柱体在刚浸没时，物体又下降4 cm，则下表面所处的深度
为h=4 cm=0.04 m，
因此刚浸没时下表面受到的液体
压强p=ρ水gh=1.0×103 kg/m3×10 N/kg×0.04 m=400 Pa.
3.
如图所示为某种型号潜水艇，其体积为5×10３ m３（海水密度近似取1.0×10３kg/m３，g取10 N/kg）.求：
（1）它在潜入到水下执行任务时所受浮力；
（2）它潜入到水下200 m时，它的一个面积为1.2 m２的舱盖所受海水的压强和压力.
难度：
知识点：压强和浮力单元测试
使用次数：200
【答案】
（1）因为潜水艇排开海水的体积等于潜水艇的体积V=5×103 m3，所以潜水艇受到的浮力：
F浮=ρgV排=1.0×103 kg/m3×10 N/kg×5×103 m3=5×107 N
（2）海水对潜水艇外壳的压强：
p=ρgh=1.0×103 kg/m3×10 N/kg×200 m=2×106 Pa
由得，F=pS=2×106 Pa×1.2 m2=2.4×106 N
4.
（2014·玉林）如图所示，体积为500 cm３的长方体木块浸没在装有水的柱形容器中，细线对木块的拉力为2 N，此时水的深度为20 cm.（g取10 N/kg），求：
（1）水对容器底的压强；
（2）木块受到水的浮力；
（3）木块的密度；
（4）若剪断细线待木块静止后，将木块露出水面的部分切去，要使剩余木块刚好浸没在 水中，在木块上应加多大的力？
难度：
知识点：压强和浮力单元测试
使用次数：2515
【答案】
（1）水对容器底的压强：
p=ρ水gh=1.0×103 kg/m3×10 N/kg×20×10-2 m=2 000 Pa；
（2）根据阿基米德原理得：
F浮=ρ水gV排=ρ水gV木
=1.0×103 kg/m3×10 N/kg×0.000 5 m3=5 N；
（3）此时木块受到三个力的作用，向上的是浮力，向下的重力和拉力，即F浮=G+F拉；
故G=F浮-F拉=5 N-2 N=3 N；
故其质量是m==
=0.3 kg；
由密度的计算公式ρ=
=
=600 kg/m3；
（4)剪刀剪断后,F′浮=G木=3 N
此时,V′排=F′浮/（ρ水g）=3/（1.0×103 kg/m2×10 N/kg）=3×10-4 m3
切去后,G′木=ρ木V木g=ρ木V′排g=0.6×103 kg/m3×3×10-4 m3×10 N/kg=1.8 N
应加的力的大小为:F′=F′浮-G′木=3 N-1.8 N=1.2 N
5.
（2014·广安）如图所示，一个圆柱形容器的底面积是10 dm2，装入一定量的水.现将一个方木块放入容器中，木块漂浮在水面上，水未溢出，木块浸入水中的体积是6 dm3， 这时水的深度为8 dm.（g取10 N/kg，ρ水=1.0×103 kg/m3）求：
（1）木块受到的浮力是多大？
（2）放入木块后，容器底部受到水
的压力是多大？
难度：
知识点：压强和浮力单元测试
使用次数：339
【答案】
（1）因为V排=V=6 dm3=6×10-3 m3，
所以F浮=ρ水gV排=1 000 kg/m3×10 N/kg×6×10-3 m3=60 N；
（2）h=8 dm=0.8 m，则水对容器底的压强：
p=ρ水gh=1 000 kg/m3×10 N/kg×0.8 m=8×103 Pa.
故F=pS=8×103 Pa×10×10-2 m2=800 N.
本卷还有3题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
8
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
7
87.5%
偏难
1
12.5%
题型统计
大题类型
数量
占比
计算题
7
87.5%
综合题
1
12.5%
知识点统计
知识点
数量
占比
压强和浮力单元测试
7
87.5%
各地中考
1
12.5%
版权提示
该作品由: 用户胡栋梁分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。