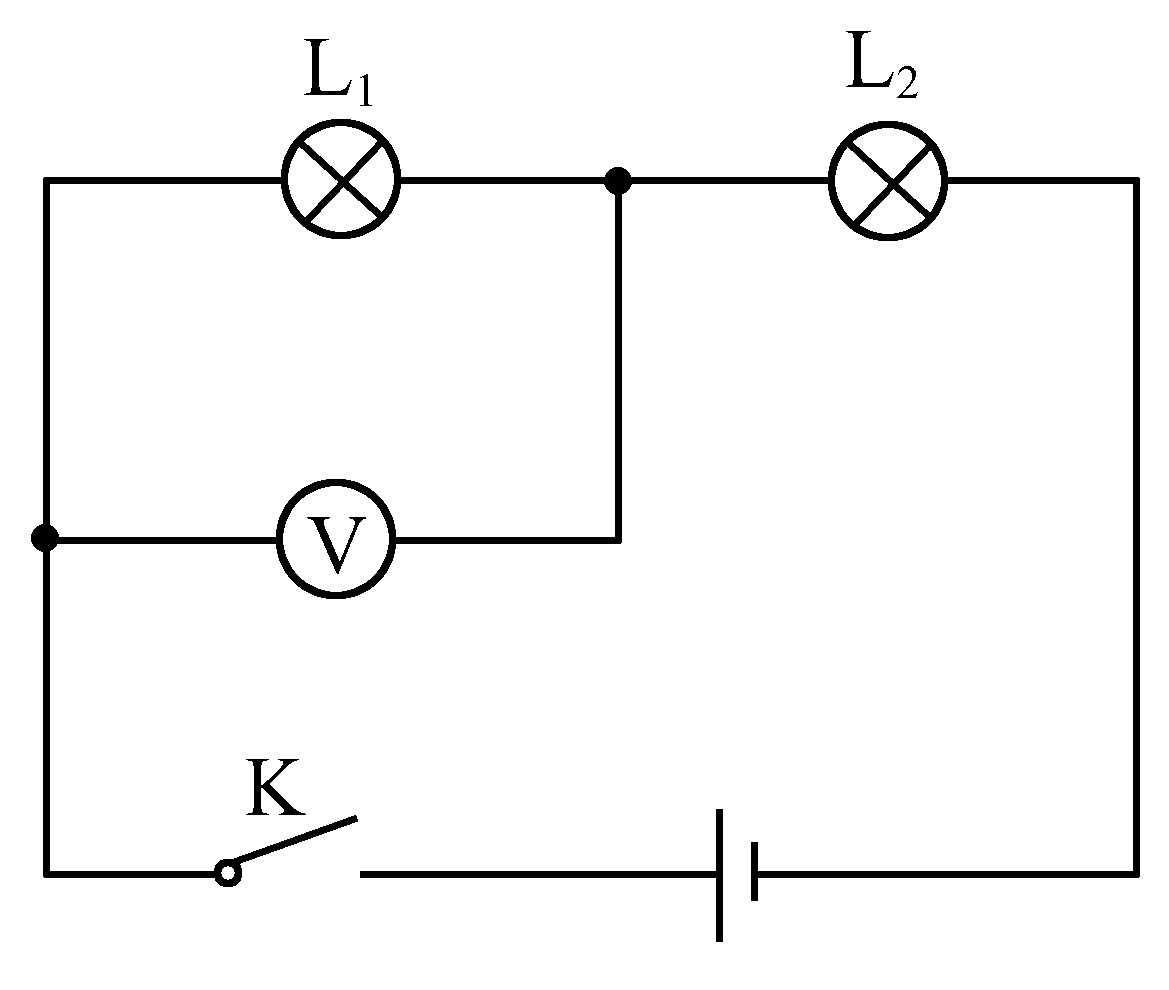
水平放置的气体阻尼器模型截面如图所示，汽缸中间有一固定隔板，将汽缸内一定质量的某种理想气体分为两部分， “H” 型连杆活塞的刚性连杆从隔板中央圆孔穿过，连杆与隔板之间密封良好。设汽缸内、外压强均为大气压强 。活塞面积为 S ，隔板两侧气体体积均为 ，各接触面光滑。连杆的截面积忽略不计。现将整个装置缓慢旋转至竖直方向，稳定后，上部气体的体积为原来的 ，设整个过程温度保持不变，求：

（ i ）此时上、下部分气体的压强；

（ ii ） “H” 型连杆活塞的质量（重力加速度大小为 g ）。

答案

（ 1 ） ；（ 2 ） ；（ 3 ） 或

【详解】（ 1 ）在 时间内，电场强度为 ，带电粒子在电场中加速度，根据动量定理可知

解得粒子在 时刻的速度大小为

方向竖直向上，粒子竖直向上运动的距离

在 时间内，根据粒子在磁场运动的周期 可知粒子偏转 ，速度反向，根据 可知粒子水平向右运动的距离为

粒子运动轨迹如图

所以粒子在 时刻粒子的位置坐标为 ，即 ；

（ 2 ）在 时间内，电场强度为 ，粒子受到的电场力竖直向上，在竖直方向

解得 时刻粒子的速度

方向竖直向上，粒子在竖直方向上运动的距离为

在 时间内，粒子在水平方向运动的距离为

此时粒子速度方向向下，大小为 ，在 时间内，电场强度为 ，竖直方向

解得粒子在 时刻的速度

粒子在竖直方向运动的距离

粒子运动的轨迹如图

在 时间内，静电力对粒子的做功大小为

电场力做正功；

（ 3 ）根据（ 1 ）问中解析有 ，

① 若粒子到达 点之前，在磁场中已经过两个半圆，则释放时刻一定在 时间内，若在 之间的 时刻释放粒子，粒子运动轨迹如图丙所示，有

，

，

，

，

，

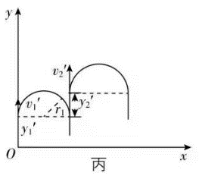
所以

整理发现

所以需满足 ，代入数据解不等式，

当 时不等式成立

② 若粒子到达 点前只经过一个半圆，则粒子在磁场中运动的轨迹半径

由 得，经第一次电场加速的末速度 ，则粒子在 时间内释放不可能，如果在 时间内释放，则第一次在电场中加速的时间 ，即在 时释放符合条件，但在此情况下， ，经过一个半圆后在电场中减速至速度为零的位移大小为

联立有

故此情况下无法到达 点，所以考虑在 时间内释放，假设粒子第一次在电场中加速的时间为 ，则 ，在此种情况下， ，经过一个半圆后在电场中减速至速度为零的位移大小为

联立有

故此情况下粒子能在 点被吸收，所以粒子释放时刻为

综上可知，在 或 时刻释放的粒子在电场存在期间被捕获