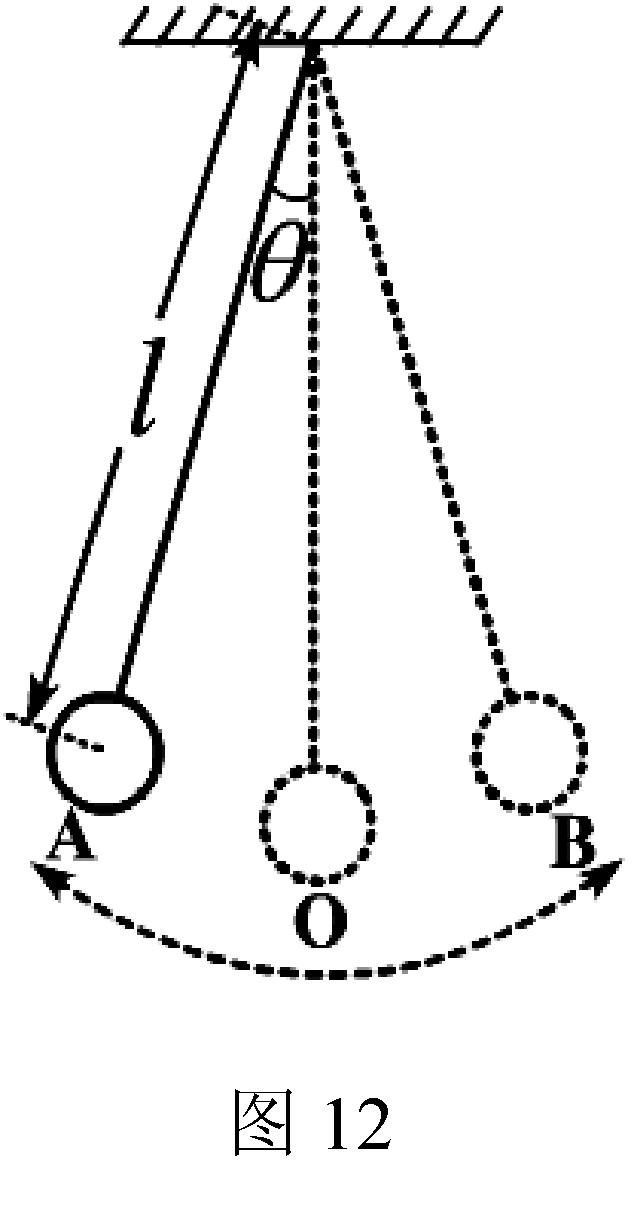
某小组三位同学发现钟摆的摆动似乎是有规律的。于是他们在细绳下面挂一小球制成了单摆，研究在摆动角度θ不大的情况下，单摆来回摆动一次所用的时间（摆动周期T）与哪些因素有关，如图12所示，l为单摆的摆长，m为单摆摆球的质量。为了减小误差，三位同学在实验中每次测量单摆摆动30次（30T）的时间。丙同学在甲、乙同学实验的基础上继续实验，三位同学的实验数据分别记录在下表中。为了进一步探究单摆的摆动规律，他们进行了适量的运算，将结果记录在下表的后三列中。
同学 | 实验 序号 | l(米) | m(克) | θ(度) | 30T （秒） |
(米2) |
[(米)1/2] |
(米·克) |
甲 | 1 | 1.0 | 30 | 4 | 60 | 1.00 | 1.0 | 30 |
2 | 1.0 | 40 | 4 | 60 | 1.00 | 1.0 | 40 | |
3 | 1.0 | 50 | 4 | 60 | 1.00 | 1.0 | 50 | |
乙 | 4 | 1.0 | 30 | 3 | 60 | 1.00 | 1.0 | 30 |
5 | 1.0 | 30 | 4 | 60 | 1.00 | 1.0 | 30 | |
6 | 1.0 | 30 | 5 | 60 | 1.00 | 1.0 | 30 | |
丙 | 7 | 0.8 | 30 | 4 | 54 | 0.64 | 0.9 | 24 |
8 | 1.0 | 40 | 4 | 60 | 1.00 | 1.0 | 40 | |
9 | 1.2 | 50 | 3 | 66 | 1.44 | 1.1 | 60 |
（1）分析比较实验序号1、2与3，可知甲同学得出的结论是：当单摆的摆长和摆动角度相同时，单摆的周期与摆球的质量____________（选填“有关”、“无关”）。
（2）分析比较实验序号4、5与6，可知乙同学研究的是：单摆的周期与摆球________________的关系，他得出的结论是：当单摆的摆长和摆球质量相同时，单摆的周期与_______________________________。
（3）分析比较实验序号7、8与9中单摆的周期与摆长的关系，可知丙同学得出的结论是：_______________________________________。
（4）进一步综合分析单摆的周期与表中后三列经运算后得到的数据关系，可归纳得出的结论是：__________________。
答案
（1）无关。
（2）摆动角度；摆动角度无关。
（3）单摆的摆长越长，单摆的周期越大。
（4）单摆的周期与
成正比。
（或：单摆的周期与
的比值是定值）
