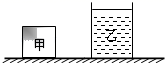
如图所示,水平地面上底面积分别为![]() 、
、![]() 的轻质圆柱形容器中分别装有甲、乙两种液体,其质量、高度的关系如表一所示.
的轻质圆柱形容器中分别装有甲、乙两种液体,其质量、高度的关系如表一所示.
| 表一 | 表二 | ||||
| 液体 | 质量 | 高度 | 液体 | 质量 | 高度 |
| 甲 |
|
|
|
|
|
| 乙 |
|
|
|
|
|

①若甲液体是水,高度为![]() 米,求水对容器底部的压强
米,求水对容器底部的压强![]() .
.
②求甲、乙两种液体的密度之比.
③现有物体![]() 、
、![]() ,其质量、体积的关系如表二所示.请在物体
,其质量、体积的关系如表二所示.请在物体![]() 、
、![]() 和液体甲、乙中各选择一个,当把物体浸沿在液体中(液体不会溢出),容器对水平地面压强变化量
和液体甲、乙中各选择一个,当把物体浸沿在液体中(液体不会溢出),容器对水平地面压强变化量![]() 、液体对容器底部压强变化
、液体对容器底部压强变化![]() .要求写出选择的液体和放入其中的物体,并求出
.要求写出选择的液体和放入其中的物体,并求出![]() 比
比![]() 的最大值.(说明:②与③小题答题所涉及的物理量均用字母表示)
的最大值.(说明:②与③小题答题所涉及的物理量均用字母表示)
答案
(1) 980Pa;(2) 4:3.(3)![]()
【解析】
【分析】
①已知水的深度,根据p水=ρ水gh求液体的压强;
②已知液体A和液体B质量相等,根液体的密度公式、V=Sh分别列出液体A和液体B质量的关系式,即可求得液体A和液体B的密度之比;
③对水平地面压强变化量△p1=![]() ;液体对容器底部压强变化量△p2=ρg△h;写出增加的压强之比,经讨论得出最大压强.
;液体对容器底部压强变化量△p2=ρg△h;写出增加的压强之比,经讨论得出最大压强.
【详解】
①若甲液体是水,高度为0.1米,求水对容器底部的压强:
p水=ρ水gh=1.0×103kg/m3×9.8N/kg×0.1m=980Pa;
②由题知,液体A和液体B的质量均为m,根据ρ=![]() 、V=Sh可得,
、V=Sh可得,
液体甲的质量:m甲=ρ甲V甲=ρ甲×S×3h,
液体乙的质量:m乙=ρ乙V乙=ρ乙×2S×2h,
则ρ甲×S×3h=ρ乙×2S×2h,
解得,甲、乙两种液体的密度之比:
ρ甲:ρ乙=4:3;
③容器对水平地面压强为固体产生的,根据p=![]() ,因轻质圆柱形容器容器,对地面的压力的增加量等于放入液体的物体的重力,
,因轻质圆柱形容器容器,对地面的压力的增加量等于放入液体的物体的重力,
对水平地面压强变化量△p1=![]() ;
;
液体对容器底部压强变化量△p2=ρg△h;
![]() =
=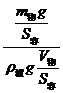 =
=![]() ,要使比值最大,故应将A物体放入乙液体中,
,要使比值最大,故应将A物体放入乙液体中,
![]() =
=![]() =
=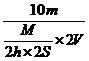 =
=![]()